RELACIONES Y PRODUCTO CARTESIANO
RELACIONES
·
Una
relación de conjunto A con un
conjunto B es el conjunto R
A
x B = R
Conjunto A por conjunto B es igual
al conjunto R (producto
cartesiano)
PRODUCTO CARTESIANO
Si tenemos dos conjuntos A y B, y
tratamos de armar todos los pares posibles formados por un elemento del
conjunto A y un elemento del conjunto B, obtendremos el producto cartesiano de los dos conjuntos.
Se escribe: A X B
Cada par que
formemos con un elemento de A y uno
de B, en ese orden, recibe el nombre de par ordenado.
Llamaremos producto cartesiano de dos conjuntos que simbolizaremos como
A X B a todos los pares de elementos ordenados que podamos formar tomando como
primer elemento un elemento del conjunto A y como segundo un elemento del
conjunto B
Ejemplo:
Sea los conjuntos:
A={1,2,3} y B={4,5,6}
Se tiene:
A X B={(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5)
,(3,6)}
El producto cartesiano A X B no
es igual al producto cartesiano B X A
B={4,5,6} y
A={1,2,3}
B X A={(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(6,1),(6,2)
,(6,3)}
MIRAR VIDEO
Del producto cartesiano A X B
se pueden extraer varias relaciones
como:
A={1,2,3} y B={4,5,6}
A X B={(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5)
,(3,6)}
1.
Conjunto de
pares ordenados, tales que la suma de sus elementos sean pares.
R={(1,5),(2,4),(2,6),(3,5)}
2.
Conjunto de
pares ordenados, tales que la suma de sus elementos sean impares.
R={(1,4),(1,6),(2,5),(3,4),(3,5),(3,6)}
LAS RELACIONES SE REPRESENTAN GRAFICAMENTE MEDIANTE
DIAGRAMA SAGITAL O EL PLANO CARTESIANO
EJEMPLO.
R={(a,3),(a,5),(b,7),(d,4),(e,6)}
MIRAR
VIDEO
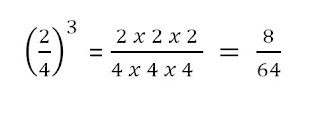
Comentarios
Publicar un comentario