POTENCIACIÓN DE NÚMEROS RACIONALES
Potenciación
de los Números Racionales
La operación de la Potenciación
no se limita únicamente a los números naturales, sino que también puede
aplicarse a los números racionales, situación en la cual cada uno de los
elementos de la fracción (numerador y denominador) es elevado a sí mismo el
número de veces que el exponente señala, es decir, que en el caso de los
números racionales, la fracción en su totalidad es considerada la base de la
potencia, aun cuando cada elemento de la fracción también puede contar con
exponentes independientes y diferentes entre si. Un ejemplo de cómo resolver
una potencia de números racionales es el siguiente:
Propiedades,
Potenciación de números racionales
Así mismo, dentro de las
operaciones de números racionales se distinguen distintas propiedades, por
medio de las cuales se rigen estos procesos matemáticos. En este sentido, se
distinguen las siguientes:
Potencia de cero
Es la propiedad que se aplica en
el caso de que una fracción se convierta en base de un exponente cero. En este
caso, la Propiedad Potencia Cero indica que el
total será siempre y en todo caso 1.
De esta forma, toda
fracción elevada a cero será uno. Por ejemplo:
Potencia de 1
También puede ocurrir que la
fracción que sirve como base de una operación de potenciación sea elevada a un
exponente 1. En este caso, el resultado coincidirá, tanto en su denominador
como en su denominador, con cada elemento de la base. Por ejemplo:
Productos de
potencias
En el caso en donde se plantee
una operación de multiplicación donde los números involucrados sean fracciones
con exponentes, se deberá tener en cuenta las siguientes particularidades:
§
Si las potencias son de igual
base: dada la operación en donde las potencias coincidan,
es decir que se trata de fracciones que coincidan, tanto en su numerador y
denominador, se procede entonces a considerar que existe una sola base, se
suman los exponentes, y el resultado se toma como el exponente final al que se
elevará cada uno de los elementos de la fracción, tal como se ejemplifica a
continuación:
§
Si la potencia tiene igual exponente: también puede ocurrir que sean los exponentes de las potencias los
que coincidan. En este caso, se toma como un solo exponente, para las potencias
sometidas a la multiplicación. Seguidamente, se multiplican de forma
correspondiente los numeradores y denominadores, y los totales son elevados a
la potencia que indica el exponente, así como se expone en el siguiente
ejemplo:
Cociente de
potencias
Así mismo, entre las distintas
potencias de números racionales puede plantearse la operación de división, en
cuyo caso pueden presentarse también distintos casos particulares, tal como se expresa a
continuación:
§
Si las potencias tienen igual base: En caso por ejemplo de que las potencias involucradas cuenten con
fracciones idénticas, es decir, que la potencia tenga igual base, se procederá
entonces a restar entre sí los exponentes,
obteniendo un total, al que serán elevados el numerador y el denominador de la
fracción, la cual se tomará como igual entre los dos términos en los que se
planteaba la división, tal como se ejemplifica en el siguiente caso:
§
Si las potencias tienen igual
exponente: Por el contrario puede ocurrir que quienes
coincidan sean los exponentes de las potencias de números racionales, sometidos
a operaciones de división. En ese caso, se toman los distintos
exponentes como uno solo, elevando posteriormente a esa potencia los
resultados correspondientes a la división de fracciones (las bases), lo cual se
hará cónsono a las Leyes matemáticas en este sentido. Un ejemplo de esto puede
ser la siguiente operación:
Potencia
de una potencia
Finalmente, otro de los casos o
propiedades que pueden darse en el caso de la potenciación de números
racionales es cuando la potencia (tanto base como exponente) es elevada a su
vez a un exponente. En este caso, las Matemáticas indican que deberá
obtenerse el total del producto entre los dos exponentes, al cual será elevado finalmente
cada uno de los elementos de la fracción. Un ejemplo de este caso puede ser el
que se ofrece a continuación:
MIRAR VIDEO
https://www.youtube.com/watch?v=AKhy5jhnefo
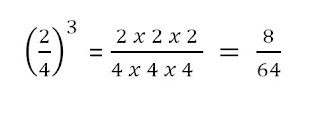







Comentarios
Publicar un comentario